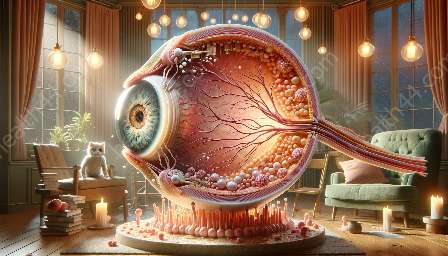
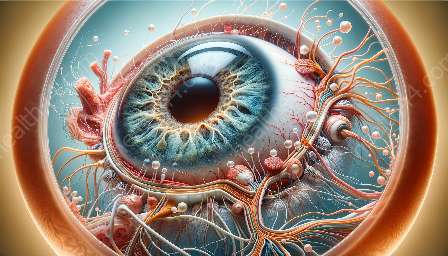
Žilnica je vaskularni sloj oka koji se nalazi između mrežnice i bjeloočnice. Ima ključnu ulogu u održavanju zdravlja i funkcije mrežnice opskrbom kisikom i hranjivim tvarima. Razumijevanje dinamike žilnice ključno je za dijagnosticiranje i liječenje raznih očnih bolesti, kao što su makularna degeneracija povezana sa starenjem i središnja serozna korioretinopatija.
Matematičko modeliranje dinamike žilnice pokazalo se moćnim alatom za proučavanje složenih mehanizama koji leže u osnovi krvotoka žilnice i njezina utjecaja na zdravlje oka. Kombinirajući matematička načela s anatomskim znanjem, istraživači mogu simulirati i analizirati ponašanje žilnice u različitim fiziološkim i patološkim uvjetima.
Anatomija žilnice
Žilnica je visoko vaskularno tkivo koje opskrbljuje vanjske slojeve mrežnice kisikom i hranjivim tvarima. Sastoji se od tri glavna sloja: koriokapilarisa, srednje velikih žila i velikih žila. Choriocapillaris se nalazi najbliže mrežnici i odgovoran je za dostavu kisika i hranjivih tvari do fotoreceptora. Srednje velike i velike žile reguliraju protok krvi i održavaju cjelokupnu prokrvljenost žilnice.
Žilnica je gusto prepuna krvnih žila i inervira ju autonomni živčani sustav. Ova složena vaskularna i neuronska mreža omogućuje žilnici da dinamički prilagodi svoj protok krvi kao odgovor na različite podražaje, kao što su promjene intenziteta svjetlosti i intraokularnog tlaka.
Matematičko modeliranje dinamike žilnice
Matematički modeli dinamike žilnice imaju za cilj uhvatiti složenu međuigru između vaskularne perfuzije, dinamike tekućine i neuralne regulacije unutar žilnice. Ovi se modeli mogu podijeliti u dvije glavne kategorije: modeli računalne dinamike fluida (CFD) i matematičke simulacije vaskularne regulacije.
Modeli računalne dinamike fluida (CFD).
CFD modeli simuliraju protok krvi unutar koroidalnih žila i razmjenu tekućine između žilnice i okolnog tkiva. Ovi modeli uzimaju u obzir geometriju koroidalne vaskulature, svojstva krvi i sile koje djeluju na vaskularne stijenke. Analizirajući hemodinamiku žilnice, CFD modeli mogu pružiti uvid u distribuciju kisika i hranjivih tvari, kao i mehanizme koji leže u osnovi bolesti žilnice.
Matematičke simulacije vaskularne regulacije
Uz CFD modele, matematičke simulacije vaskularne regulacije usredotočuju se na neuralne i biokemijske mehanizme koji kontroliraju protok krvi u žilnici. Ovi modeli uključuju utjecaj autonomnih neurotransmitera, lokalnih metabolita i vazoaktivnih tvari na vaskularni tonus žilnice. Integriranjem fizioloških i farmakoloških podataka, ove simulacije mogu razjasniti regulacijske putove uključene u koroidalnu perfuziju i vazomociju.
Značaj za očnu patologiju
Razumijevanje dinamike žilnice kroz matematičko modeliranje ima izravne implikacije na dijagnozu i liječenje očnih bolesti. Na primjer, matematički modeli mogu pomoći u rasvjetljavanju patofiziologije središnje serozne korioretinopatije, stanja koje karakterizira žarišna hiperpermeabilnost koroide i nakupljanje subretinalne tekućine. Simulacijom dinamike tekućine unutar žilnice istraživači mogu steći uvid u čimbenike koji pridonose napredovanju bolesti i razviti ciljane terapijske strategije.
Slično tome, matematičko modeliranje koroidne cirkulacije relevantno je za makularnu degeneraciju povezanu sa starenjem, vodeći uzrok gubitka vida kod starijih osoba. Integriranjem genetskih i okolišnih čimbenika rizika u prediktivne modele, istraživači mogu identificirati pojedince s visokim rizikom razvoja koroidne neovaskularizacije i voditi provedbu preventivnih mjera.
Buduće smjernice
Područje matematičkog modeliranja dinamike žilnice spremno je za daljnji napredak, potaknut integracijom naprednih tehnika snimanja, računalnih metoda i pristupa modeliranju s više skala. Modaliteti snimanja visoke razlučivosti, kao što je angiografija optičke koherentne tomografije, daju detaljne anatomske i hemodinamske informacije koje se mogu ugraditi u matematičke modele. Nadalje, upotreba personaliziranih računalnih modela temeljenih na podacima o pojedinačnim pacijentima obećava za optimizaciju dijagnoze i liječenja koroidnih poremećaja.
Zaključno, matematičko modeliranje dinamike koroide nudi snažan okvir za razotkrivanje zamršenosti koroidalne cirkulacije i njezine uloge u okularnoj fiziologiji i patologiji. Koristeći matematičke principe i anatomske uvide, istraživači mogu steći dublje razumijevanje složene međuigre između vaskularne perfuzije, dinamike tekućine i neuralne regulacije unutar žilnice, u konačnici utirući put inovativnim dijagnostičkim i terapijskim strategijama.